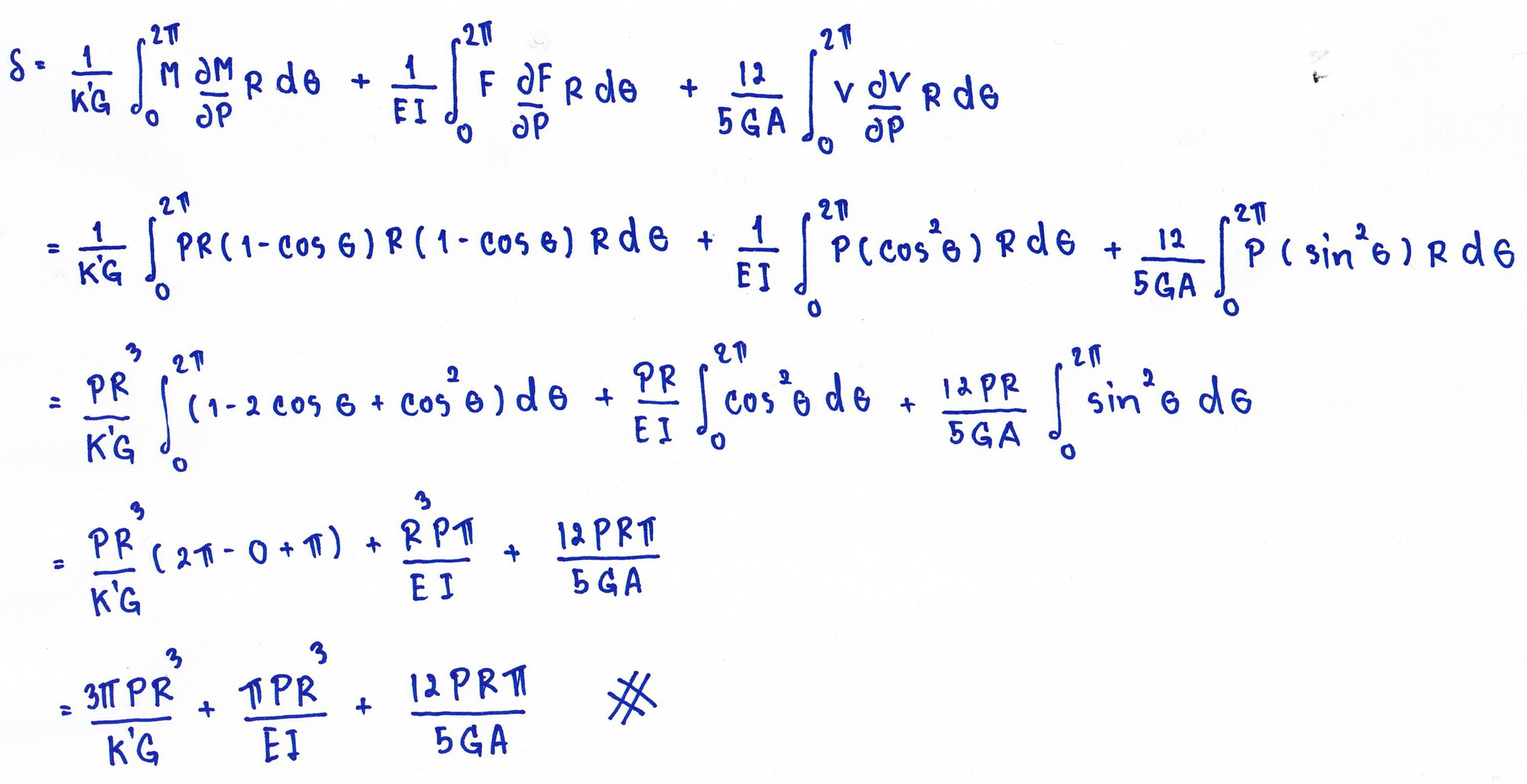|
|
|
|
|
| |
|
3.PROBLEMS 5.21 |
| |
|
|
|
|
5.21 :
|
|
The helical lock washer in figure P5.21 has material elastic properties of E and G, and cross-sectional properties of A,I,and K'(J if the section is circular).What is its spring rate with respect to the force P,which tends to flatten it? You may neglect terms expected to be unimporatant , but enumerate terms neglected. |
|
|
Solution : |
| |
|
|
Known : |
|
The general geometry and force of separation for a spring rate with respect to the force P,which tends to flatten it? |
|
|
|
Find : |
|
Develop an expression relating separating force and deflection. |
|
|
|
Assumpions : |
|
1.The deflections are elastic |
|
|
2.The ring remains in the plane of the applied loads. |
|
|
|
| |
|
Schematic and Given Data: |
| |
|
| |
Analysis: |
|
1.A typical segment of the ring bounded by angle  (defined in the figure) as a free body. The deflection has three companents: those caused by bending, axial lond (compression in the bottom half ,tension in the top ),and transverse shear.comrresponding equations are (defined in the figure) as a free body. The deflection has three companents: those caused by bending, axial lond (compression in the bottom half ,tension in the top ),and transverse shear.comrresponding equations are |
| |
M = PR ( 1 - cos  ) |
F = P cos  |
V = F sin  |
| |
| |
|
2.The preceding equations are valid for all values of .Hence,we can integrate from 0 to 2 |
| |
|
|
| |
|
|
comments : |
|
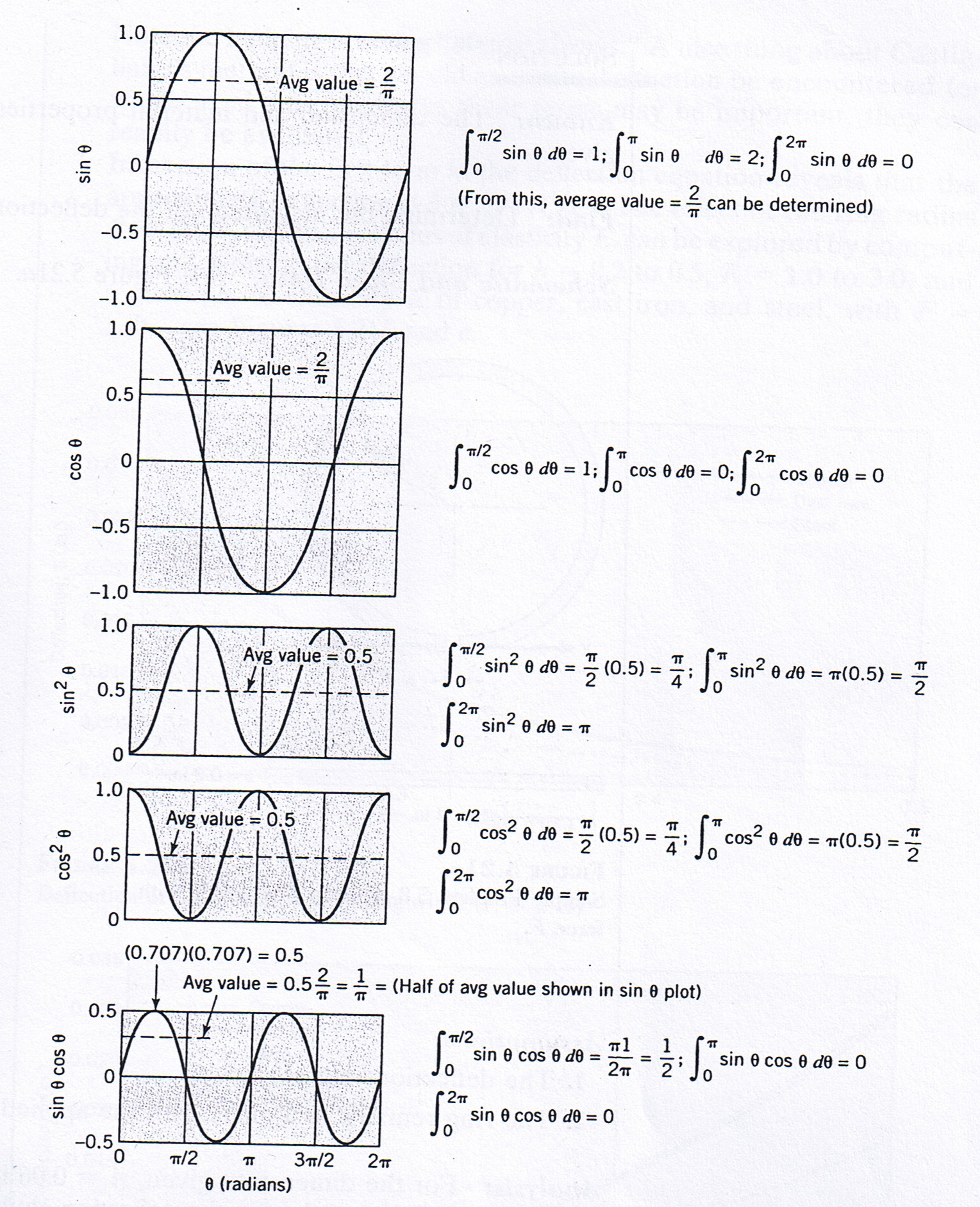
1.In the preceding solution the values of the definite integrals were written directly, without the bother ( and possibility for error )of integrating the expressions and then substituting upper and and lower limits. Evaluation of definte integrals such as these as these can be accomplished expediently by taking advantageof the elementary graphical interpretations in Figure.Such figures can be reproduced readily from the simplest concepts of integral calculus ,thereby avoiding dependence on memory or integral tables. |
| |
|
|
|
|
|
2.Note that the ring is symmetrical about the vertical but not the horizontal axis. Hence, we could have integrated between 0 and  and then doubled each integrat, but we could not have in tegrated between 0 and and then doubled each integrat, but we could not have in tegrated between 0 and  /2 and then multiplied by 4. /2 and then multiplied by 4. |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
| |
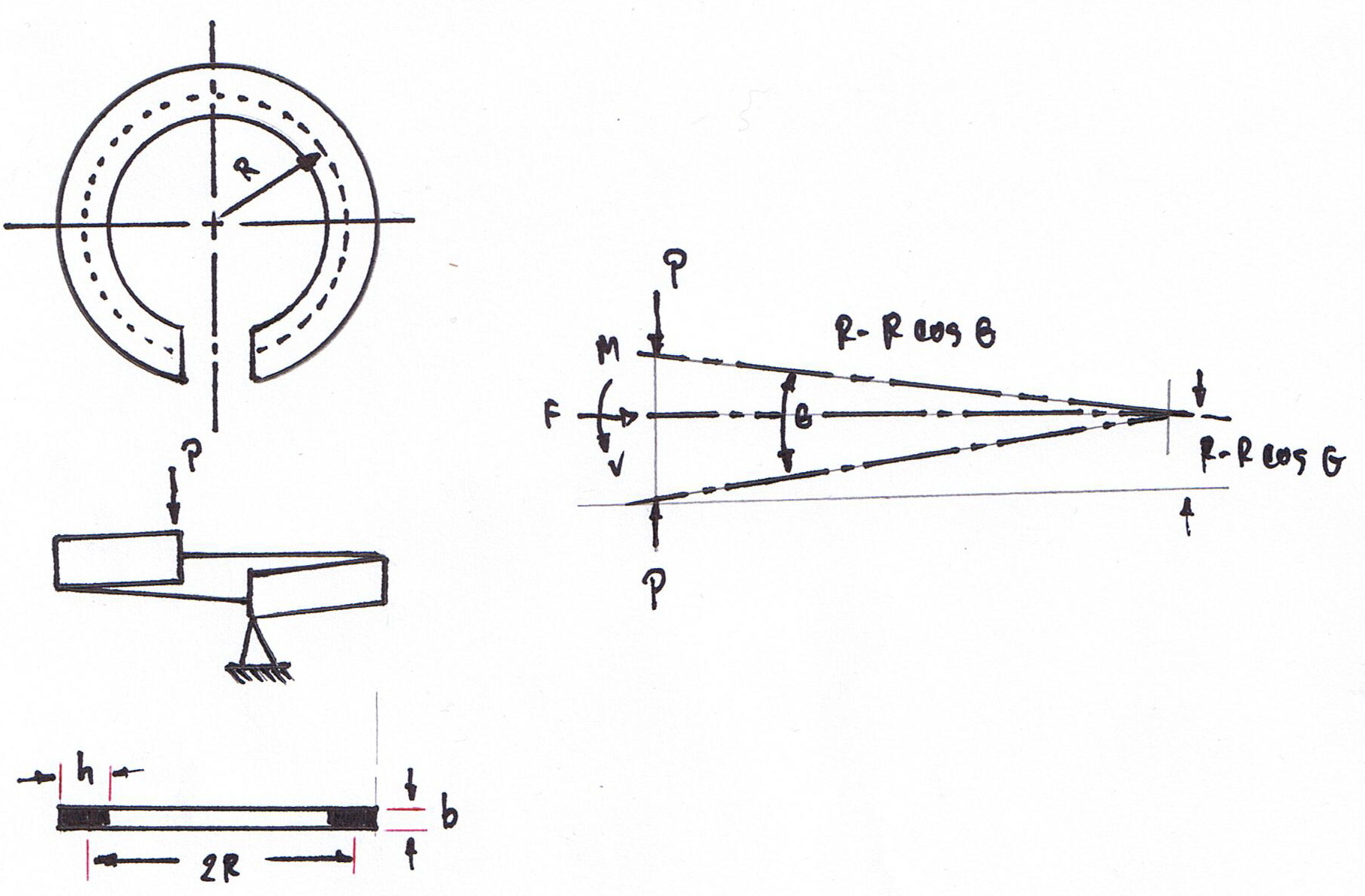
 (defined in the figure) as a free body. The deflection has three companents: those caused by bending, axial lond (compression in the bottom half ,tension in the top ),and transverse shear.comrresponding equations are
(defined in the figure) as a free body. The deflection has three companents: those caused by bending, axial lond (compression in the bottom half ,tension in the top ),and transverse shear.comrresponding equations are  )
)